1° PARADOSSO

Salviati incomincia a sbalordire  i suoi interlocutori con un argomento paradossale:
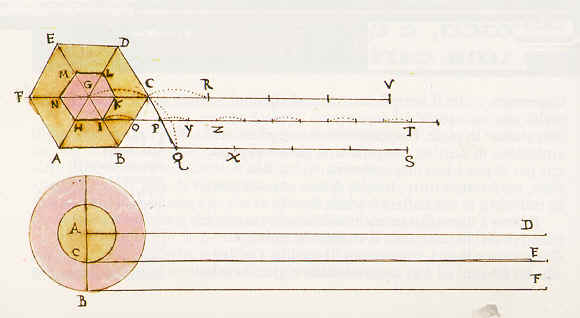
Presi due esagoni regolari concentrici, li fece rotolare sopra una linea AS; finita "l' intera conversione",

• il poligono maggiore avrà percorso su AS sei linee uguali, senza interposizioni, pari al suo perimetro,

• il poligono minore avrà ugualmente impresso sei linee uguali, cioè un segmento HT quasi uguale ad AS, ma interrotte da sei archi ( IO, PY, ...); infine il centro G avrà toccato la linea GV solo in sei punti.

• Che cosa accade se il poligono ha centomila lati, oppure se prendiamo due cerchi concentrici?
   
• Compiuta una rivoluzione, che linee avranno percorso il cerchio minore e il centro?

riproduzione dell'esperienza

Galileo-Salviati risponde che se avessimo un poligono con centomila lati, la linea percorsa dal poligono maggiore sarebbe uguale a quella percorsa dal poligono minore " ma con l'interposizione di centomila spazi vacui trasposti ".

Se si ripete il ragionamento nel caso dei cerchi, anche le linee BF, CE e AD percorse rispettivamente dal cerchio maggiore, dal minore e dal centro sarebbero uguali.

Salviati si domanda:

Nel caso dei cerchi - che sono poligoni con infiniti lati - la linea "passata" dagli infiniti lati del cerchio grande è uguagliata da quella passata dagli infiniti lati del cerchio minore, ma con l'interposizione di altrettanti, cioè infiniti, spazi vacui:

Galileo afferma che sia le semplici linee, sia le superfici e i corpi solidi vanno considerati "composti di infiniti atomi non quanti". In tale modo potè giustificare il paradosso della linea percorsa dalle due circonferenze.

Ricordiamo che già Aristotele, nei Mechanica, affrontò questo problema detto della "ruota", che veniva enunciato così: " ...entrambi (i cerchi), se concentrici, compiono la medesima rotazione, se invece separati ne compiono due diverse." La giustificazione che diede Galilei a questo problema non lasciò soddisfatti i suoi contemporanei (in particolare Descartes lo criticò aspramente) e produsse alcune perplessità anche tra i suoi allievi e amici.